LÍMITE DE UNA FUNCIÓN
Para las matemáticas, un límite es una magnitud fija a la que se aproximan cada vez más los términos de una secuencia infinita de magnitudes. Función, por su parte, también coincide con el término anterior en lo que respecta a su origen. Y es que, de igual modo, viene del latín, más exactamente de “functio”, que es sinónimo de “función o ejecución”. La expresión límite de una función se utiliza en el cálculo diferencial matemático y refiere a la cercanía entre un valor y punto. Por ejemplo: si una función f tiene un límite X en un punto t, quiere decir que el valor de f puede ser todo lo cercano a X que se desee, con puntos suficientemente cercanos a t, pero distintos. En definitiva, una función f con límite X en t quiere decir que dicha función tiende hacia su límite X cerca de t, con f(x) tan cerca de X como sea posible pero haciendo que x sea distinto de t. De todas maneras, la idea de cercanía es poco precisa, por lo que una definición formal requiere de más elementos
Ejemplos:
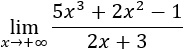
Solución Tenemos la indeterminación infinito partido infinito. Como el grado del polinomio del numerador es mayor que el del denominador, el límite es infinito
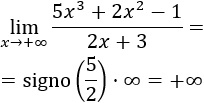
El infinito es positivo porque el cociente de los coeficientes principales de los polinomios es positivo. Límite 2
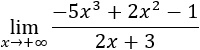
Solución